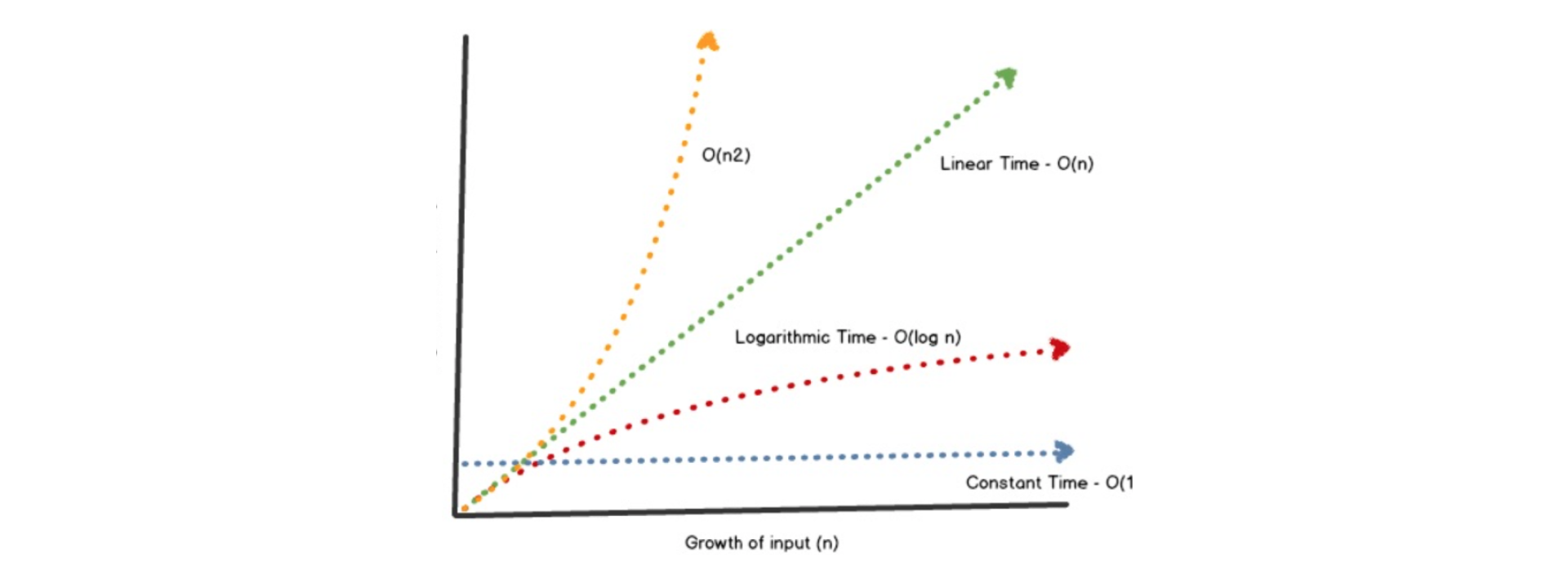
Big O notation deals with the time and space complexity of an algorithm. Big O notation forms the basis of analyzing an algorithm in computer science and programming. We only focus on the time aspect when analyzing an algorithm.
Big O notation is one of the most important aspects to understand and master. Even experienced programmers lack an understanding of it.
Big O notation describes the worst-case scenario and it will always assume the upper limit where the algorithm performs the maximum number of iterations. For example, consider the following Python function in the code snippet below, the worst-case scenario for this algorithm will be that the input array doesn't contain an 'x'.
def checkIfArrayContainsX(arr):
for i in range(len(arr)):
if arr[i] == 'x'
return True
return False
As a programmer with a good grasp of mathematics, the best way to understand Big O notation is through code examples. Let's go over some order of growths of Big O notation.
O(1)
O(1) describes an algorithm that will always execute in the same amount of time regardless of the input data set size. See the following code snippet:
def returnFistElement(a):
# return the first element of the array passed
return a[0
O(N)
O(N) describes an algorithm whose performance increases linearly in direct proportion to the size of the input data set size. Go back and see the first code snippet, the execution time will increase as the size of the input data set increases.
O(N^2)
O(N^2) describes an algorithm whose performance is directly proportional to the square of the size of the input data size. It normally occurs in an algorithm containing nested loops. See code snippet below.
def ifArrayItemMatch(arr1, arr2):
for i in range(len(arr1)):
for j in range(len(arr2)):
if(arr1[i] == arr2[j]):
return True
return False
O(2^N)
O(2^N) denotes an algorithm whose growth doubles with each addition to the input data set. Fibonacci is an example of O(2^N).
def Fibonacci(num):
if num <= 1:
return num
return Fibonacci(num - 2) + Fibonacci(num - 1)
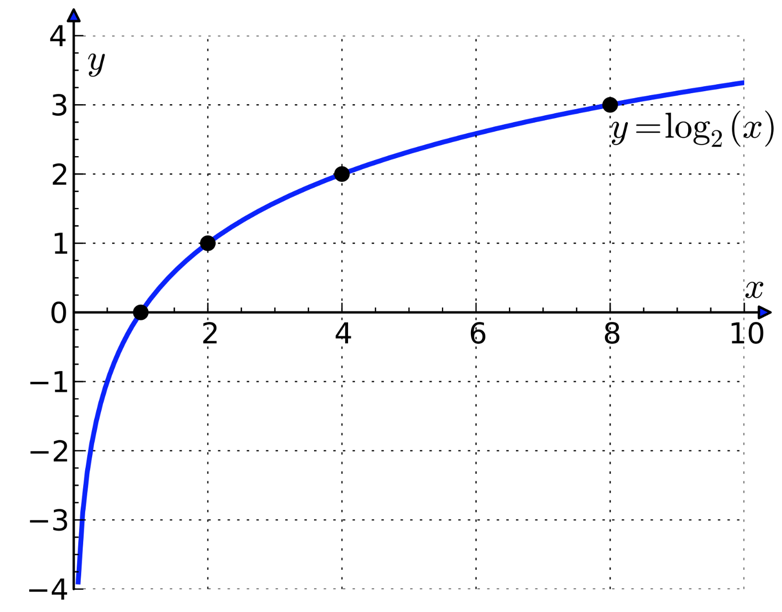
O(logN)
O(logN) produces logarithmic curves that peak at the beginning and then slowly flattens out. An algorithm like binary search has an O(logN) growth factor.
TLDR
Big O notation deals with the time complexity of an algorithm. Some of the common orders of growth as O(1), O(N), O(N^2), O(2^N) and O(logN).